[Contents]
양자역학의 의미,
에르빈 루돌프 요제프 알렉산더 슈뢰딩거,
Schrödinger equation,
시간에 무관한 슈뢰딩거 방정식- time independent Schrodinger equation,
시간에 의존하는 슈뢰딩거 방정식- time dependent Schrodinger equation
● 양자역학(Quantum Mechanics)의 의미
양자역학은 고전역학에 대비되는 개념으로, 고전물리학인 뉴턴의 역학에서는 물질을 입자로만 간주하며, 관찰 대상의 초기상태와 가해지는 힘을 알면 미래의 상태(위치, 운동량 등)을 예측할 수 있었습니다.
이 접근은 꽤나 유효했으며 오랫동안 진리로 받아들여졌습니다.
그러나 과학 기술의 발전과 함께 연구가 미시세계로 더욱 확장되면서 고전역학으로는 설명할 수 없는 현상들이 발견되었고, 이에 따라 양자역학의 필요성이 부각되었습니다.
(양자역학 관련 아래 글 참조)
[KOR] [공학,과학] 양자역학 (I) (tistory.com)
[KOR] [공학,과학] 양자역학 (I)
[Contents] - 양자역학(Quantum Mechanics) 이란 - 주요특징(양자화, 파동-입자 이중성, 불확실성원리,고전역학과의 차이점) - 히스토리 - 양자역학의 형성 양자역학(Quantum Mechanics)은 미시적인 계의 현상을
raykim81.tistory.com
양자역학은 고전역학과 구별되는 중요한 특징을 가지고 있습니다.
이론에 따르면 물질은 입자적이면서 파동적인 성질을 동시에 가지며, 관측 대상을 정확하게 측정하는 것이 불가능하며 오로지 확률적으로만 나타납니다.
양자역학은 아인슈타인의 광전효과 실험, 드 브로이의 물질파 이론, 하이젠베르크의 불확정성 원리와 같은 많은 과학자들과 연구들에 의해 발전해왔습니다.
고전역학은 양자역학의 특수한 경우로 볼 수 있으며, 양자역학을 통해 모든 고전역학적 상황을 해결할 수 있습니다.
그러나 이러한 변환은 복잡하고 어려운 작업이므로, 대개의 경우 고전역학을 사용하여 문제를 해결하려고 합니다.

에르빈 루돌프 요제프 알렉산더 슈뢰딩거
(독일어: Erwin Rudolf Josef Alexander Schrödinger, 1887년 8월 12일 - 1961년 1월 4일)는 노벨상을 수상한 오스트리아-아일랜드 물리학자로서 양자역학에서 여러 가지 근본적인 결과들을 개발했다.
슈뢰딩거 방정식은 시스템의 파동 함수를 계산하고 시간에 따라 어떻게 동적으로 변하는지를 계산하는 방법을 제공한다.
그는 과학, 고대 및 동양 철학 개념, 윤리 및 종교의 철학적 측면에 큰 관심을 기울였다.
그는 또한 철학과 이론 생물학에 관해 저술했다. 슈뢰딩거의 고양이 사고 실험으로도 유명하다.
슈뢰딩거는 폴 디랙과 함께 여러 대학에서 교수로 일생의 대부분을 보내며 양자역학 연구로 1933년에 노벨 물리학상을 수상했고, 같은 해에 나치즘에 반대하여 독일을 떠났다.
개인적인 삶에서 그는 아내와 정부와 함께 살았으며 이로 인해 문제가 발생하여 옥스퍼드에서 자리를 떠나게 되었다. 그 후 1938년까지 그는 오스트리아의 그라츠에서 지위를 유지하다가 나치가 점령하자 도망쳤고 마침내 더블린에서 장기 정착을 찾아 1955년 은퇴할 때까지 머물렀다. 그는 73세에 결핵으로 빈에서 사망했다.
● 슈뢰딩거 파동방정식(Schrodinger's Wave Equation)의 의미
우리가 알 수 있는 것은 전자의 위치에서 발견될 확률뿐입니다.
이것은 파동과 같은 형태로 나타나며 파동방정식을 따릅니다.
이때 중요한 개념인 슈뢰딩거 파동 방정식이 양자역학적 관점에서 물질의 상태를 설명하는 방정식으로 등장합니다.
이 방정식은 고전역학에서의 힘-가속도 법칙에 버금가는 중요한 역할을 합니다.
다시 말하면, 양자역학의 핵심 원리 중 하나인 것이죠.
양자역학에서 물질은 입자성과 파동성을 동시에 갖는다고 이야기합니다.
이것이 바로 양자역학의 핵심입니다. 이 개념을 수학적으로 나타내면 파동방정식이 됩니다. 이 방정식은 전자의 위치와 에너지를 확률적으로 표현하는데 사용됩니다. 원자핵 주변에서 또는 전자가 돌고 있는 궤도의 위치를 수학적으로 나타내는 데 슈뢰딩거 방정식을 활용할 수 있습니다.
또한, 정확한 위치를 알 수 없는 이유는 하이젠베르크의 불확정성 원리로 설명됩니다.
고전물리학에서는 입자적 표현으로 특정 궤도에서 돌고 있다고 생각하지만, 현대 물리학에서는 파동적 표현으로 특정 궤도 위에서 존재한다고 이해합니다.
결국, 이 미분방정식의 해를 찾는 것이 목적이며, 이 해는 파동함수(Wave Function)로 알려져 있습니다. 파동함수는 시간과 공간에 따라 변하는 함수로, 전자의 위치와 에너지에 대한 확률 분포를 나타내며, 각각은 독립적으로 시간과 위치에 대한 전자의 가능성을 나타냅니다.
슈뢰딩거 파동방정식을 간략하게 설명하자면, 이는 파동의 에너지 보존 법칙을 나타내는 양자역학적 미분방정식이라고 할 수 있습니다.
Schrödinger equation
양자역학적 관점에서 물질의 상태를 기술하는 방정식이다.
취리히 대학교 교수였던 오스트리아의 빈 출신 물리학자 에르빈 슈뢰딩거가 1926년 발표하였다.
고전적인 운동 방정식과 슈뢰딩거 방정식은 기초적인 방정식이라는 공통점 외에 많은 차이가 있다. 그중 특히 유념해야 할 큰 차이로 두 방정식이 다루는 대상이 있다. 고전적인 운동 방정식에서는 입자 혹은 질점의 위치나 운동량같이 의미가 직관적으로 잘 와닿는 것을 대상으로 하는 데 반해 슈뢰딩거 방정식은 다소 추상적인 파동함수라는 것을 다룬다. 그리고 이 파동함수는 추상적인 만큼 그 의미에 해석이 필요하다. 예를 들자면 파동함수가 물리적인 실체인가 아닌가 하는 부분이나 측정이 도대체 어떤 식으로 양자상태를 붕괴시키는지는 양자 역학의 해석에 따라 설명이 갈린다. 그러나 이러한 해석 방법에 관계없이 파동함수로부터 어떤 측정 결과의 확률분포를 알 수 있다는 것만은 기본적인 가정(혹은 해석에 따라 가정으로부터 다다를 수 있는 현상)이다. 이는 실험적으로도 잘 증명되어 있다. 따라서 파동함수가 물리적 실체인지 아닌지는 불확실하더라도 양자역학을 세우는 데 필수적임은 확실하다.
사실 고전역학보다 양자역학이 훨씬 근본적인 법칙이기에 이 방정식으로도 당연히 고전역학적인 문제를 풀 수 있으며, 양자역학의 고전역학 근사(플랑크 상수를 0으로 보내는 등)를 취하면 당연히 구해지는 답도 고전역학에서 구한 값과 일치한다. 다만 고전적 풀이보다 훨씬 어렵고 복잡하기에 실용적으로 쓰이는 경우가 드물 뿐이다. 자세한 내용은 물질파, 양자역학 항목을 참고.
개요
- 시간에 무관한 슈뢰딩거 방정식- time independent Schrodinger equation

- 시간에 의존하는 슈뢰딩거 방정식- time dependent Schrodinger equation

슈뢰딩거 방정식이란 복소 파동함수의 에너지, 위치, 시간에 관련된 편미분 방정식을 말한다.
쉽게 말하자면 고전 역학에서 와 같은 것이다.
이를 이용해서 여러 포텐셜 상황에서의 파동함수와 파동함수의 에너지를 계산할 수 있다.
우선 파수가 이고 각진동수가 인 시간과 위치에 대한 1차원 파동함수는 아래와 같다.
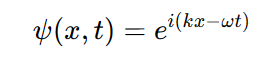
식을 간단히 하기 위해서 앞의 상수는 생략, 드브로이 관계식은 아래와 같다.
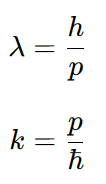
플랑크의 흑체복사와 아인슈타인의 광전효과에서 아래의 관계식을 얻는다.
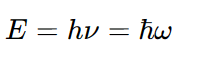
는 입자의 진동수이다.
양자역학은 파동함수와 연산자, 고유값 방정식을 통해 기술되므로 이를 이용해서 슈뢰딩거 방정식을 유도하겠다.
시간에 무관한 슈뢰딩거 방정식
고유함수를 파동함수 로 갖고, 고유값을 의 에너지 로 가지는 에너지 연산자 를 얻는 것이 목적이다.
입자의 에너지는 운동에너지+포텐셜에너지이므로
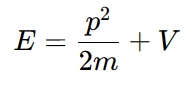
드브로이 관계식에 의해 이므로
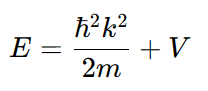
양변에 파동함수 를 곱하면
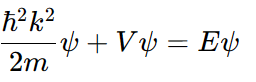
이때 파동함수에 대입하면
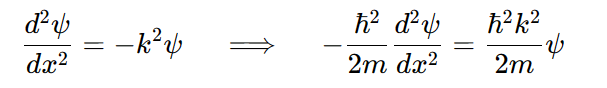
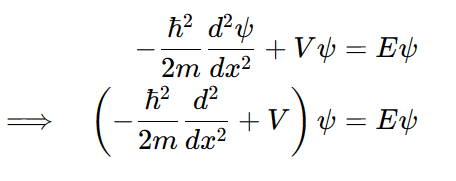
위 식을 시간에 무관한 슈뢰딩거 방정식이라 부른다.
또한 에너지를 얻는 에너지 연산자
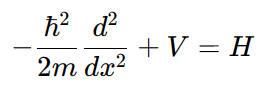
를 간단히 라고 표기하고 해밀토니안이라 한다.
3차원일 경우 해밀토니안과 슈뢰딩거 방정식은 다음과 같다.
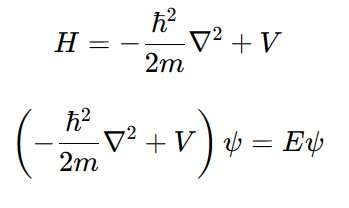
를 사용하여 시간에 무관한 슈뢰딩거 방정식을 간단히 표현하면
시간에 의존하는 슈뢰딩거 방정식에 의하면 입자의 에너지는 각진동수 와 플랑크 상수 ℏ로 표현된다.
각진동수는 파동함수을 시간에 대해서 미분했을 때 얻을 수 있다.
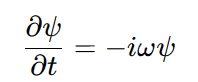
따라서
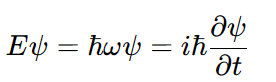
이를 첫 식에 대입하면 시간에 의존하는 슈뢰딩거 방정식을 얻는다.

'공학,과학' 카테고리의 다른 글
| [KOR] [공학,과학] TEC(ThermoElectric Cooler), 제벡효과, 펠티어효과 (50) | 2023.10.29 |
|---|---|
| [KOR] [공학,과학] 초전도체의 현상과 LK-99의 논란 (20) | 2023.10.27 |
| [KOR] [공학,과학] 양자역학 (I) (37) | 2023.10.05 |
| [KOR] [과학,공학] FIB (Focused Ion Beam) (76) | 2023.09.04 |
| [KOR] [상식] 미사일과 로켓 (위성발사체) (86) | 2023.09.01 |